[영리한 프로그래밍을 위한 알고리즘] #10 힙의 응용

---

우선순위 큐(priority queue)

일반적인 큐는 선입선출로 부가적인 조건 없이 먼저 들어온 데이터가 먼저 나가는 구조지만 우선순위 큐는 들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나오는 것이다.

종류에는 최대 우선순위 큐와 최소 우선순위 큐가 있다. 두 가지 방식은 부호에만 차이가 있으며 알고리즘은 동일하다.

Max Heap을 이용하여 최대 우선순위 큐를 구현해본다.

최대 우선순위 큐

새로운 원소를 삽입하고 꺼낼 때는 최대값을 삭제한 뒤 반환한다.

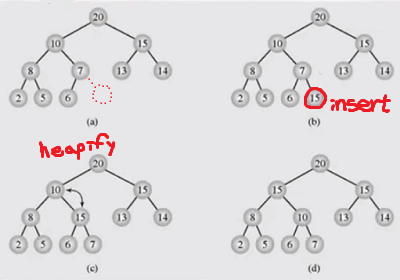
Insert Max Heap 구조를 유지하면서 새로운 값을 삽입하기 위해서는 고려할 점이 두가지 있다.

• 완전 이진 트리 구조를 깨지 않는 노드에 삽입한다.

• 삽입한 값이 heap property를 깨지 않게 위치 교환이 필요하다.

수도 코드

Max-Heap-Insert(A, key) {
  // 힙 크기를 증가 시켜준다.
  heap_size = heap_size + 1;
  // 그리고 마지막 위치에 우선 값을 넣는다.  
  A[heap_size] = key;
  // 삽입한 값의 노드 i
  i = heap_size;
  // i > 1 : 루트노드가 아니다.
  // A[Parent(i)] : 부모 노드에 저장된 값
  while ( i>1 and A[Parent(i)] < A[i] ) {
    // 값 비교해서 더 크면 위치 교환함
    exchange A[i] and A[Parent(i)];
    // 삽입한 값의 노드 이동
    i = Parent(i);
  }
}

시간복잡도는 O(h)로 트리의 높이와 비례한다.
힙 구조에서 트리의 높이는 노드의 개수가 n일 때 높이는 logn이므로 시간복잡도는 O(logn)이다.

Extract
값을 제거하고 반환한다. 최대 우선순위 큐 이므로 항상 최대값만을 추출한다.

max heap 이기 때문에 최대값은 항상 루트에 위치하기 때문에 최대값을 찾는것은 간단하다. 하지만 노드를 제거해야하기 때문에 주의해야한다.

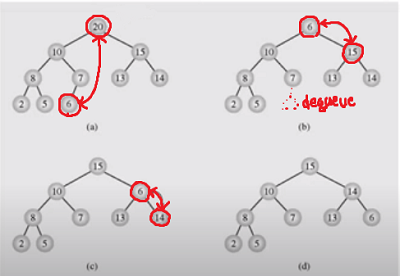
노드를 삭제해도 힙 구조가 깨지지 않는 곳은 마지막 노드이다. 따라서 마지막 노드의 데이터를 유지하면서 노드를 삭제시켜야한다.

• 루트 노드와 마지막 노드의 데이터 교환

• 마지막 노드 삭제, 반환

• heap property 깨지않게 데이터 위치 조정

수도 코드

Heap-Extract-Max(A) {
  // 예외처리
  if heap-size[A] < 1
    then error "heap underflow"
  // 최대값을 저장
  max <- A[1]
  // 마지막 노드를 루트로
  A[1] <- A[heap-size[A]]
  // 힙 사이즈 감소시킴
  heap-size[A] <- heap-size[A] - 1
  // heapify 진행
  Max-Heapify(A, 1)
  // 최대값 반환
  return max
}