[자료구조]트리 구조

---

트리(tree)

나무의 가지처럼 계속해서 뻗어나가는 모습처럼 생겼기 때문에 트리라는 이름으로 불린다.

하나의 루트(root) 노드가 자식 노드를 가지고 그 자식 노드들도 자식노드들을 가지면서 뻗어가는 구조이다. 이런 구조는 탐색에서 큰 장점을 가지는데 선형 구조의 경우 특정 데이터를 검색하면 전체 구조를 순회하여야 하지만 트리의 경우 자식의 수로 분기를 나눌 수 있고 탐색과정을 줄일 수 있게 된다.

용어 정리

• 노드(node)
  트리 구조의 각 요소

• 루트 노드(root node) 부모 노드가 없는 최상위 노드

• 리프 노드, 단말 노드(leaf node/ terminal node)
  자식 노드가 없는 최하위 노드

• 내부 노드, 비단말 노드(internal node/ non-terminal node)
  단말 노드를 제외한 모든 노드 (루트 노드를 포함)

• 간선(edge)
  노드와 노드를 잇는 선

• 레벨(level) 또는 높이
  부모 노드와 자식 노드간의 계층

• 형제 노드(sibling node)
  같은 부모 노드를 가지는 그 자식 노드

• 깊이(depth)
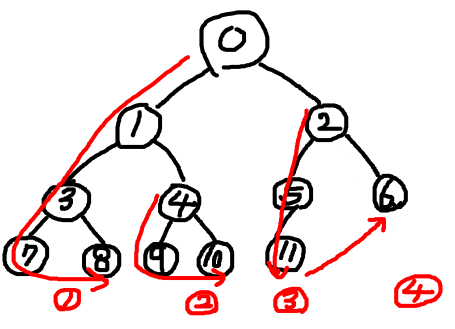
  트리에서 노드가 가질 수 있는 최대 level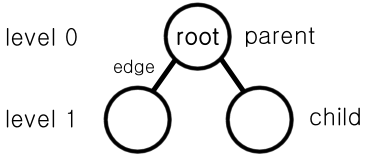

  

트리 종류

트리는 자식 노드의 수 또는 구조에 따라서 여러 종류가 있다.

이진 트리(binary tree)

각 노드가 최대 두 개의 자식을 가지는 트리를 말한다. 최대 노드의 수가 세 개 이상이면 삼진 트리(ternary tree) 그 이상의 개수를 가진다면 다중 트리라 부른다.

• 이진 탐색 트리(binary search tree)

  모든 왼쪽 자식들 <= n < 모든 오른쪽 자식들

  즉 이진 트리 구조안에 데이터들은 오름차순이나 내림차순으로 정렬이 되어있어야하며 조건을 만족한다면 원하는 데이터를 찾을 때 까지 범위를 반으로 줄이면서 탐색하기 때문에 빠른 성능을 보인다.

• 완전 이진 트리(complete binary tree)
  노드가 왼쪽부터 채워진 형태의 트리를 말한다.

• 정 이진 트리(full binary tree)
  트리의 모든 노드가 0개 또는 2개의 자식을 가지는 구조를 말한다. 즉 자식 노드를 가진다면 최대 개수를 채우거나 하나도 가지지 않는 경우를 말한다.

• 포화 이진 트리(perfect binary tree) 모든 내부 노드가 두 개의 자식 노드를 가지는 트리이다.

트리 구현

이진 탐색 트리를 구현해본다.

• 모든 원소는 서로 다른 유일한 키를 가진다.

• 왼쪽 노드는 부모의 값보다 작다.

• 오른쪽 노드는 부모의 값보다 크다.

삽입

#include <iostream>

using namespace std;

class Node
{
public:
	int data;
	Node* leftNext;
	Node* rightNext;

	Node(int _data, Node* _left, Node* _right)
	{
		data = _data;
		leftNext = _left;
		rightNext = _right;
	}
};

Node* Insert(Node* _node, int _data)
{
	if (_node == NULL)
	{
		_node = new Node(_data, NULL, NULL);
		return _node;

	}
	else
	{
		if (_data < _node->data)
		{
			_node->leftNext = Insert(_node->leftNext, _data);
		}

		else
		{
			_node->rightNext = Insert(_node->rightNext, _data);
		}
	}
	return _node;
}

넣으려는 데이터와 노드에 저장된 데이터를 비교하여 작으면 왼쪽 크면 오른쪽으로 배치한다.

이렇게 구조를 만들면 특정 값을 검색할 때 노드를 지날 때마다 검색할 요소의 개수가 1/2씩 감소하기 때문에 빠른 검색이 가능하게 된다.

삭제
트리의 노드를 삭제할 때 확인해야할 경우

• 자식이 없는 노드
  추가적인 작업이 필요없이 해당 노드를 삭제하면 된다.

• 자식이 하나인 노드
  삭제한 노드자리에 그 자식을 올려준다.

• 자식이 두개인 노드
  왼쪽의 자식 중 가장 큰 값, 오른쪽 자식 중 가장 작은 값을 올려준다.

  이 조건만 만족 시켜도 그 아래 자식 노드들이 보존된다.

Node* Remove(Node* _node, int _data)
{
	Node* curr = NULL;

	if (_node == NULL)
	{
		return NULL;
	}

	// 데이터 크기 비교, 작으면 다음 왼쪽노드, 크면 다음 오른쪽 노드
	if (_data < _node->data)
	{
		_node->leftNext = Remove(_node->leftNext, _data);
	}
	else if (_data > _node->data)
	{
		_node->rightNext = Remove(_node->rightNext, _data);
	}
	
	// 데이터 동일한 경우
	else
	{
		// 노드의 자식이 둘 다 존재할 때
		if (_node->leftNext != NULL && _node->rightNext != NULL)
		{
			// 오른쪽 노드에서 최소값 노드 검색
			curr = findMinimum(_node->rightNext);
			// 자식 노드의 값을 저장한다.    
			_node->data = curr->data;
			// 값을 옮긴 자식의 노드를 제거 시도한다.  
			_node->rightNext = Remove(_node->rightNext, curr->data);
		}
		else
		{
			// 자식 노드들이 옮겨지고 빈 노드를 제거해준다.  
			curr = (_node->leftNext == NULL) ? _node->rightNext : _node->leftNext;
			delete _node;
			_node = NULL;
			return curr;
		}
	}

	return _node;
}

트리 순회

트리를 순회하는 방법은 3가지가 있다.

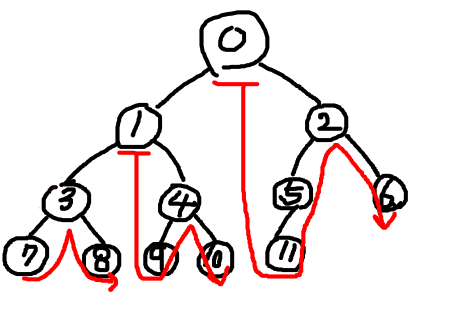
• 전위 순회(preorder traversal)

  

  뿌리 > 왼쪽 자식 > 오른쪽 자식 순서대로 순회한다.

  0 > 1 > 3 > 7 > 8 > 4 > 9 > 10 > 2 > 5 > 11 > 6

  뿌리부터 시작해서 각 노드의 왼쪽을 우선적으로 순회한 다음 오른쪽 자식으로 넘어간다.

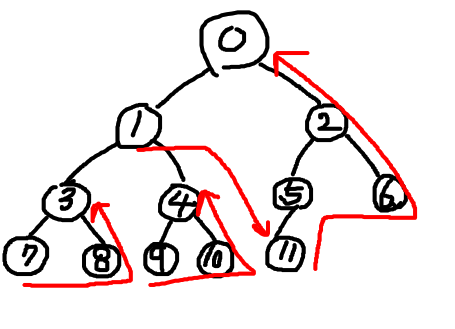
• 중위 순회(inorder traversal)

  

  왼쪽 자식 > 뿌리 > 오른쪽 자식 순서로 순회한다.

  7 > 3 > 8 > 1 > 9 > 4 > 10 > 0 > 11 > 5 > 2 > 6

  가장 왼쪽의 노드부터 시작한다. 그 다음 부모 노드를 방문하고 오른쪽 노드로 넘어간다. 서브 트리의 방문이 끝나면 서브트리의 부모를 방문하고 다시 그 자식의 가장 왼쪽부터 시작한다.

• 후위 순회(postorder traversal)

  

  왼쪽 자식 > 오른쪽 자식 > 뿌리 순서로 순회한다.

  7 > 8 > 3 > 9 > 10 > 4 > 1 > 11 > 5 > 6 > 2 > 0

  왼쪽 자식부터 시작해서 오른쪽 자식 부모 노드 순서로 순회하고 마지막에 루트 노드로 간다.

순회
재귀호출로 처리한다.

PrintNode(Node* _node)
{
	if (_node == NULL)
	{
		return;
	}

	// 전위식 
	void Preorder(Node* _node)
	{
		if (_node == NULL)
		{
			return;
		}

		printf("%d ", _node->data);
		
		// 전위식
		printf("%d ", _node->data);
		PrintNode(_node->getLeft());
		PrintNode(_node->getRight());

		// 중위식 
		PrintNode(_node->getLeft());
		printf("%d ", _node->data);
		PrintNode(_node->getRight());

		// 후위식
		PrintNode(_node->getLeft());
		PrintNode(_node->getRight());
		printf("%d ", _node->data);
	}

}

출력 코드는 재귀함수의 특징을 활용한 방법이다.